AAA树
引入
在学习了 $LCT$ 之后,树上一些常见的问题已经不能满足选手们的需求,从而出现了这样一道题:
[bzoj3153]Sone1
它要求选手们维护子树覆盖,子树加,子树最值,子树和,链覆盖,链加,链最值,链和,换父亲,换根这十二个基本操作
假如没有换父亲的确是树链剖分的基本操作
假如没有子树修改与查询的确是 $LCT$ 的基本操作
然而现在都有了
于是就有了 $AAA$ 树和 $toptree$ 来解决上述问题,由于笔者现在并不会后者,因此该篇文章主要讲述 $AAA$ 树的原理与实现
原理
$LCT$ 无法解决子树问题的原因是它只维护了实链的信息而子树问题要涉及到虚子树的信息
在静态树问题中,有链分治这种分治方法,其原理是用不同的数据结构对重链和实链分开进行维护并及时合并轻重链信息
考虑对每个 $LCT$ 上的点建一个数据结构来统计其虚子树的信息,它要具备如下功能:
- 能够快速删除与加入新的节点
- 能够快速合并其管辖点的信息
不难想到建出一棵平衡树来维护其虚子树的信息,在这里笔者选择使用 $splay$ ,我们将原树进行改造,使得每个点 $p$ 有四个儿子,其中 $son_{p,0/1}$ 表示维护其实链 $LCT$ 的儿子,而 $son_{p,2/3}$ 分别是维护其虚子树的 $splay$ 的根,对于维护虚子树的节点,我们强制其在 $splay$ 的叶节点,下面是一个简单的例子:
原树: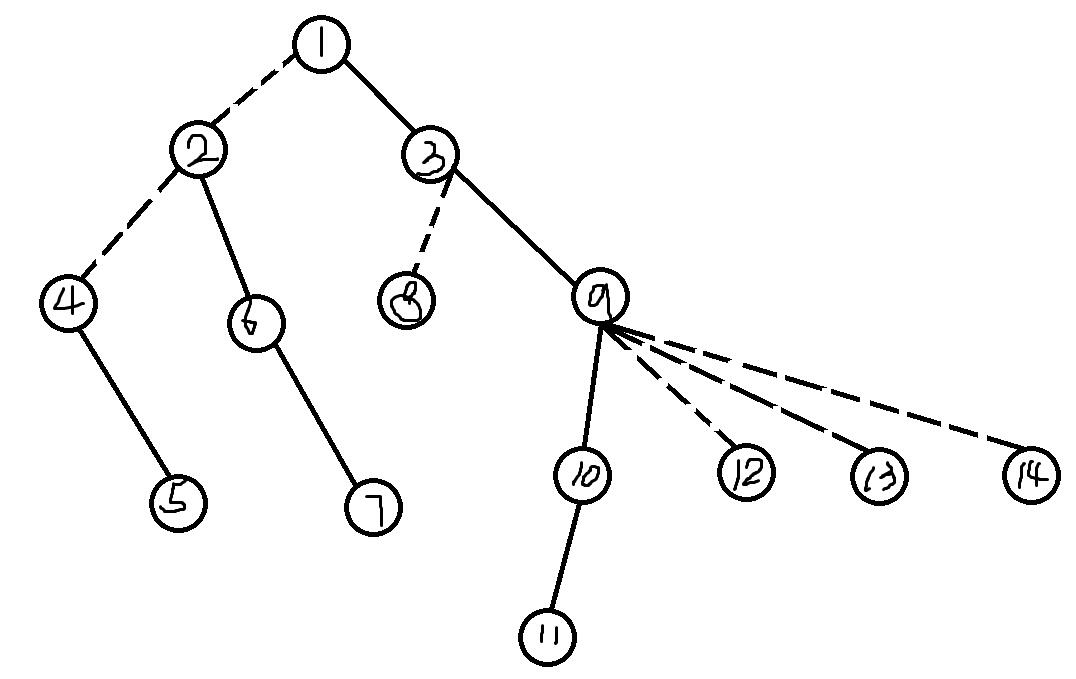
$AAA$ 树: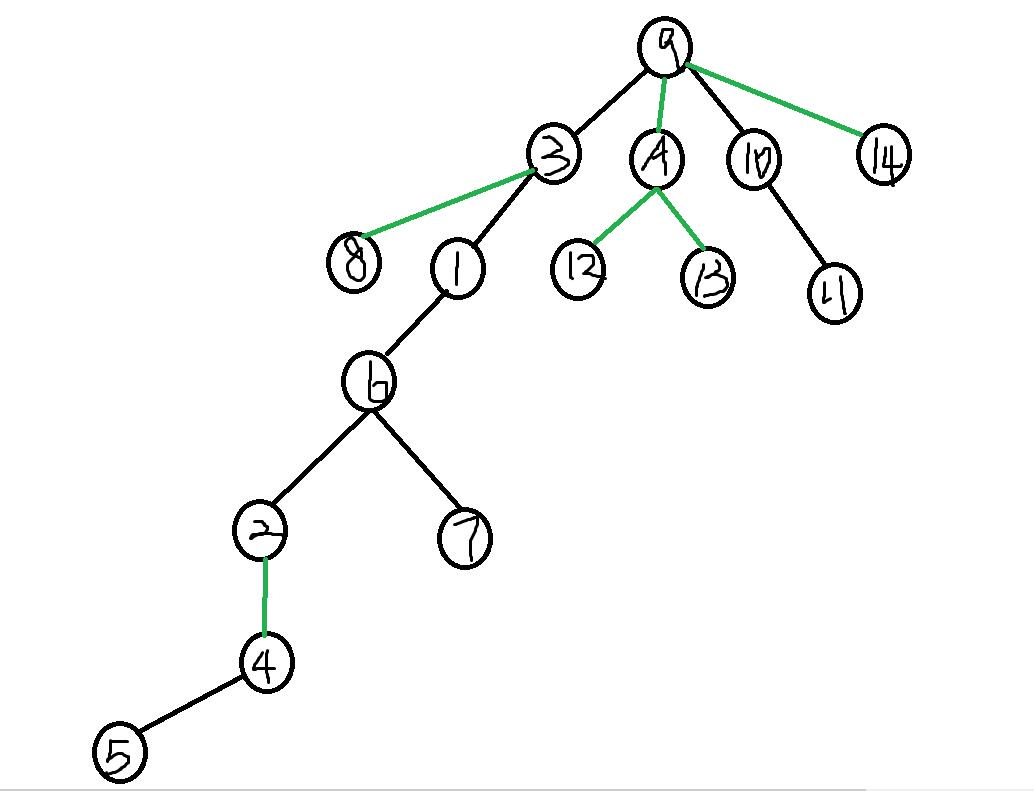
现在要实现加点和删点进其虚儿子所在的 $splay$
加点:将该点插入 $splay$ 中(可能会新建一个如上图中的 $A$ 节点)
删点:若该点父亲是 $A$ 点,就删掉该点和其父亲,并将自己的兄弟放到父亲的位置,否则直接删掉该点即可
然后 $access$ 操作就直接在换右儿子的时候利用上述两个函数即可,加点对应将实边换成虚边,删点对应将虚边换成实边
维护标记:
每个节点记录以下三种信息: $cha,sub,all$ 表示实链的信息,整棵实 $splay$ 上面挂着的所有虚子树的信息,以及整棵子树的信息
$pushup$ 操作:
简单易懂
先要维护两个维护树形态的标记: $rev,inr$
分别表示翻转标记以及其是否是 $A$ 点
然后要维护两个标记 $All,Cha$
$All$ 表示对整棵子树进行的修改,但不修改实链的信息, $Cha$ 表示对实链进行修改
$All$ 标记在传实儿子的时候不修改链,在传虚儿子的时候要修改链
$cut(v)$ 操作: $access(fa_v)$ ,然后在其虚 $splay$ 中删掉 $v$
$link(u,v)$ 操作:$access(v)$ ,然后把 $u$ 加进其虚 $splay$ 中
链操作同 $LCT$ ,不过只跟 $cha$ 有关
子树操作:修改/查询点 $u$ 的时候,直接 $access(u)$ ,然后其子树信息都在虚 $splay$ 中,用 $u$ 的单点信息和其虚子树信息拼接起来即可
这样就可以尝试解决该题或者直接去世了
