多项式的运算
多项式的加减法,数乘
这个大家应该都会吧
不推了。
多项式乘法
这个大家应该都会吧
还是推一推吧。
已知的:
$A(x)=\sum_{i=0}^na_ix^i$
$B(x)=\sum_{i=0}^mb_ix^i$
要求的:
$C(x)=A(x)B(x)=\sum_{i=0}^{n+m}(\sum_{j=0}^{min\{i,n\}}a_j\times b_{i-j})x^i$
显然直接暴力做是$O(n^2)$的,考虑如何优化。
那么我们使用$fft$或者$ntt$来实现点值表示法和系数表示法之间的快速转化。
为了方便起见,我们将$A,B$的最高次数统一成一个$2$的幂(对于超过$n/m$的项的系数看成0即可)
所谓的系数表示法就是我们平常用的那种。
而点值表示法,就是把这个多项式理解成一个函数,用这个函数上的若干个点的坐标来描述这个多项式:
$f(x)=(x_0,y_0),(x_1,y_1),…,(x_n,y_n)=p_0,p_1,p_2,…,p_n$
假设我们已经将$A,B$两个函数转化成了点值表示,于是就可以马上求出$C$的点值表示:
$A(x)=(x_{a,0},y_{a,0}),(x_{a,1},y_{a,1}),…,(x_{a,n-1},y_{a,n-1})=p_{a,0},p_{a,1},…,p_{a,n-1}$
$B(x)=(x_{b,0},y_{b,0}),(x_{b,1},y_{b,1}),…,(x_{b,n-1},y_{b,n-1})=p_{b,0},p_{b,1},…,p_{b,n-1}$
那么$C(x)=p_{a,0}\times p_{b,0}, p_{a,1}\times p_{b,1},…,p_{a,n-1}\times p_{b,n-1}=p_{c,0},p_{c,1},…,p_{c,n-1}$
然后再把$C(x)$还原成系数表达式即可。
注意:我们需要保证$x_{ai},x_{bi}$互不相同
现在就只用考虑如何实现点值表示和系数表示的互换了。
也就是如何用更少的计算次数来求出$n$个不同的$x$值对应的$y$值。
考虑有一个具有特殊性质的东西:单位根
单位根保证了$w_n^0,w_n^1,…,w_n^{n-1}$是互不相同的并且有$w_n^{ij}=(w_n^i)^j$
而原根在模数为质数$p$的时候也有$g^0,g^1,g^2,…,g^{n-1}$是互不相同的并且$g^{ij}\equiv (g^i)^j \mod p$
这满足了我们上面的性质,因此我们考虑将$w_n^0,w_n^1,…w_n^{n-1}$作为$x_0,x_1,…x_{n-1}$带入求点值。
然后要用到两个引理:
- 折半引理:$w_n^{k\times 2}=w_{\frac n2}^k$(n为偶数 )
- 消去引理:$w_n^{k}=-w_n^{k+\frac n2}$
这两个引理可以画个单位圆简单证明
然后利用按照下标的奇偶性来进行分治处理:
$f(x)=\sum_{i=0}^na_ix^i$
$\Rightarrow f(w_n^k)=\sum_{i=0}^na_i w_n^{ik}$
$\Rightarrow f(w_n^k)=\sum_{i=0}^{\frac n2-1}a_{2i}w_n^{2ik}+w_n^k\sum_{i=0}^{\frac n2-1}a_{2i+1}w_n^{2ik}$
同时又有:
$f(w_n^{k+\frac n2})=\sum_{i=0}^{\frac n2-1}a_{2i}w_n^{2ik}-w_n^k\sum_{i=0}^{\frac n2-1}a_{2i+1}w_n^{2ik}$
这一步需要用到引理
所以我们只要算出两个重新分配了系数的多项式的值就可以了。
显然一直分下去只有$log$层。
于是总时间复杂度$O(nlogn)$
注意到递归的效率很低,我们可以预处理最后一层的系数的位置然后用迭代的方式还原回去来优化常数
原理:
我们发现分治完之后相当于将$i$和$i$对应的二进制数在$lim$下反转之后对应的新二进制数$i’$这两个位置的系数$a_i,a_i’$交换了位置。
这就成功的实现了系数转点值。
下面来看点值转系数:
注:下面的图片有几点没写清楚:
- 最后的时候$e_{i,i}=0,e_{i,j|i\not=j}$
- 那个$I_n$指的就是 $n\times n$ 的单位矩阵。
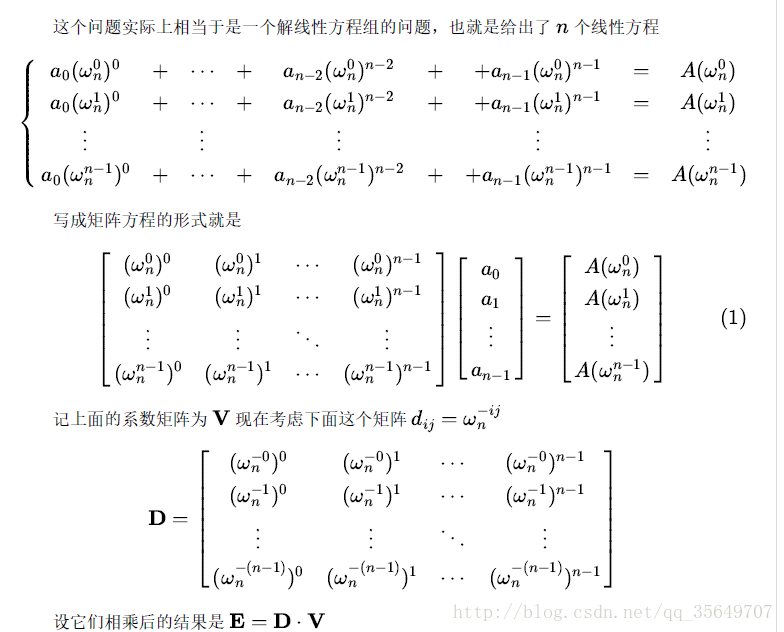

以上是$fft$的证明,$ntt$同理。
多项式求逆
- 定义:
对于一个多项式$A(x)$,如果存在一个多项式$B(x)$,满足$B(x)$的次数小于等于$A(x)$且$A(x)B(x)≡1 \mod x^n$,那么我们称B(x)为$A(x)$在模$x^n$意义下的逆元,简单记作$A^{−1}(x)$ - 求法:
$n=1?$那不就是$c$的逆元么。
$n>1?$我们令$B(x)=A^{-1}(x)$
那么有$A(x)B(x)\equiv 1 \mod x^n$
然后可以用类似倍增的方法求。
假设我们已经知道$C(x)$满足$A(x)C(x)\equiv 1\mod x^{\frac n2}$(这里的$\frac n2$都是向上取整)
显然$A(x)B(x)\equiv 1\mod x^{\frac n2}$是成立的。
我们将两式相减:
$A(x)(B(x)-C(x))\equiv 0\mod x^{\frac n2}$
所以$B(x)-C(x)\equiv 0\mod x^{\frac n2}$
然后将两边平方:
$B^2(x)-2B(x)C(x)+C^2(x)\equiv 0\mod x^{\frac n2}$
=>$B^2(x)-2B(x)C(x)+C^2(x)\equiv 0\mod x^n$
这一步很关键,请神犇们仔细思考原因
然后两边同时乘上$A(x)$
=>$B(x)-2C(x)+A(x)C^2(x)\equiv 0\mod x^n)$
于是$B(x)\equiv2C(x)-A(x)C^2(x)\mod x^n$
乘法可以用$fft/ntt$加速,因为每次递归的时候多项式最高次项都减少一半,所以总复杂度仍然是 $O(nlogn)$
一道板题:洛谷4238
多项式求导
默认大家都会函数求导
这个多项式求导属于最简单的那一种
对于一个多项式$f(x)=\sum_{i=0}^na_ix^i$
它求导的结果$f’(x)=\sum_{i=0}^{n-1}(i+1)a_{i+1}x^i$
于是直接模拟即可。
多项式积分
相当于是多项式求导的逆运算。
对于一个多项式$f(x)=\sum_{i=0}^na_ix^i$
它求导的结果$\int\mathrm f(x)dx=\sum_{i=1}^{n+1}\frac{a_{i-1}}ix^i$
可以看出来一个函数的导函数积分起来等价于自己。
多项式取对
我们令$g(x)=lnf(x)$
那么根据链式法则求导知:
$g’(x)=\frac{f’(x)}{f(x)}$
我们已经会多项式求逆和多项式积分,多项式求导了,于是就成功解决了多项式取对。
多项式取exp
这个时候我们要提到一个重要的方法:牛顿迭代法
假设我们要求$h(B(x))\equiv A(x) \mod x^n$中的$B(x)$
现在考虑构造有一个以多项式为变量的函数$g(f)=h(f)-A$
那么要求的就是$g(f)$模$x^n$意义下的零点。
假设已经求出了$g(f)$模$x^{\left\lfloor\frac x 2\right\rfloor}$的零点$f_0$
那么现在$g(f_a)=g(f_0)+g’(f_0)(f_a-f_0)+\frac{g’’(f_0)}2(f_a-f_0)^2+…$
由于$f_0$是模$x^{\left\lfloor\frac
x 2\right\rfloor}$的零点,所以有:
$g(f_a)\equiv g(f_0)+g’(f_0)(f_a-f_0)\equiv0\mod x^{n}$
所以移项后发现$f_a=f_0-\frac{g(f_0)}{g’(f_0)}$
这个东西有什么用呢?
我们简单举个例子:
比如说多项式求逆,可以构造$g(f)=\frac1f-A$,算出来$f_a=2f_0-Af_0^2$。
再比如说现在要求的多项式取$exp$:
构造$g(f)=e^f-A$,算出来$f_a=f_0(1-lnf_0+A)$
然后就做完了。
多项式开方
直接使用上面所说的牛顿迭代的结论,令$g(x)=f^2-A$,带入得到:$f_a=\frac{f_0^2+A}{2f_0}$
然后用多项式求逆搞一搞即可。
多项式的除法/取模
现在有两个多项式:
$A(x)=\sum_{i=0}^na_ix^i,B(x)=\sum_{i=0}^mb_ix^i,n>m$
要求出$C(x)=\sum_{i=0}^{n-m}c_ix^i,D(x)=\sum_{i=0}^td_ix^i,d<m$,满足$A(x)=B(x)C(x)+D(x)$,其中$C(x)$类比商,$D(x)$类比余数。
感觉想法比较神奇。
对于一个多项式$f(x)$,我们定义一个$f_R(x)$表示将这个多项式的系数翻转之后得到的新多项式,如$f(x)=2x^3+3x^2+x+5$时,$f_R(x)=5x^3+x^2+3x+2$
然后可以惊奇的发现:$f_R(x)=x^nf(\frac1x)$
然后就有$A(\frac 1x)=B(\frac 1x)C(\frac 1x)+D(\frac 1x)$
所以$x^nA(\frac 1x)=x^nB(\frac 1x)C(\frac 1x)+x^mD(\frac 1x)$
所以$A_R(x)=B_R(x)C_R(x)+D_R(x)\times x^{n-m}$
因此$A_R(x)\equiv B_R(x)C_R(x)\mod x^{n-m}$
所以$C_R(x)\equiv A_R(x) (B_R(x))^{-1} \mod x^{n-m}$
$D(x)=A(x)-B(x)C(x)$
分治FFT
一个\times 听起来挺高大上\times 的东西,然而很简单。
前置知识:cdq分治,fft
考虑这样一个转移式子$f_0=0,f_i=\sum_{j=1}^if_{i-j}g_j$,其中$g$数组已知,让你求$f$数组。
容易观察到,这个转移式是一个卷积的形式。
然而并不能直接$fft$因为$f$的转移跟自身有关,当然你可以使用我们马上下面讲的生成函数秒掉。
生成函数做法
我们对$f,g$构造生成函数$F(x),G(x)$
那么$F(x)-f_0=G(x)F(x)$
所以$F(x)=\frac{f_0}{G(x)-1}$,直接上多项式求逆即可,时间复杂度为$O(nlog_n)$吊打分治FFT。
新的做法:分治FFT
假设现在要求的$f$值的下标为$[l,r]$,我们可以利用类似$cdq$分治的思想,先递归求出$[l,mid]$这一段的$f$值,然后考虑$[l,mid]$对$[mid+1,r]$的贡献,最后递归$[mid+1,r]$即可。
那么现在要考虑的就只有$[l,mid]$对$[mid+1,r]$的贡献啦!
对于$f_i,i\in[mid+1,r],f_j,j\in[l,mid],f_i+=f_j\times g_{i-j}$,然后把所有的放在一起考虑就成了一个卷积的形式。
于是我们将$f_{l,l+1,…,mid}$构成的多项式和$g_{0,1,…,r-l}$构成的多项式乘起来更新$f_{mid+1,mid+2,…,r}$即可。
然而时间复杂度为$O(nlog^2_n)$
生成函数
- 前置知识:泰勒展开
我对于生成函数的理解:生成函数就相当于对一个集合的表示:
一般生成函数(Ordinary Generating Function) 也就是大家常说的$OGF$:
$F(x)=\sum_{i=0}^{\infty}a_ix^i$
指数生成函数(Exponential Generating Function) 也就是大家常说的$EGF$:
$F(x)=\sum_{i=0}^{\infty}a_i\frac{x^i}{i!}$
它们可以帮助我们处理一些组合问题。
两个经常用到的公式:
$1+x+x^2+…=\frac{1}{1-x}$
$1+x+x^3+…+x^n=\frac{1-x^{n+1}}{1-x}$小学的等比数列求和公式
以及我们的泰勒展开公式。
解决组合问题的时候我们通常将$x^i$的系数看成值为$i$的数被凑出的方案数
事实上,我认为加法原理和乘法原理在生成函数上同样对应了具体的运算。
比如说现在我们要从集合$A_1,A_2,A_3,..,A_n$中选一个值为$i$的数出来问有多少种选法(加法原理),那么考虑这$n$个生成函数的和$C$,$C$中$x^i$的系数就是答案。
再比如说我们要从$A_1,A_2,A_3,…,A_n$中各选一个数加起来,问加和为$i$的方案数(乘法原理),那么考虑这$n$个生成函数的积$C$,$C$中$x^i$的系数就是答案。
是不是有点感觉了?
我们举一个例子:正整数集$N=\{1,2,3,4,…\}$,元素的大小定义为它的数值,定义$SEQ(A)$ 是由$A$的元素排成的序列组成的集合,一个序列的大小定义为其元素大小总和,现在让我们求一求$SEQ(N)$。
$SEQ(N) = \{正整数有序拆分\}=\{0,1,1+1,2,1+1+1,1+2, 2+1,3\}$
考虑构造一个函数$N(x)=x+x^2+…=\frac x{1-x}$
于是$SEQ(N)=1+N(x)+N^2(x)+…=\frac 1{1-N(x)}=1+\frac x{1-2x}=1+x+2x+4x^2+…$
是不是感觉挺好用的
两道板题:bzoj3028,poj3734
多项式多点求值
现在已知$f(x)=\sum_{i=0}^na_ix^i$与$m$个数$b_1,b_2,…,b_m$。
求$f(b_1),f(b_2),…,f(b_m)$
有很显然的$O(nm)$暴力做法,这里直接略过。
考虑构造一个函数$g_{l,r}(x)=\prod_{i=l}^r(x-b_i)$
那么$\forall x_0\in[l,r]$,有$f(x_0)=(f\%g_{l,r})(x_0)$
证明:
令$f(x)=g_{l,r}(x)\times B(x)+R(x)=(x-x_0)\times (\frac{g_{l,r}(x)}{x-x_0}\times B(x))+R(x)$
当$x=x_0$时:$f(x_0)=0+R(x_0)=R(x_0)=(f\%g_{l,r})(x_0)$
有了这个结论就可以分治处理了。
多项式快速插值
给出$n$个点$(x_i,y_i)$,求对应多项式。
有一种叫做拉格朗日插值的东西需要了解一下。
并且要会上面的多项式多点求值。
仔细观察拉格朗日插值的代数式:
考虑如何快速求$val_i=\prod_{j=\not i}(x_i-x_j)$
构造函数$M(x)=\prod_i(x-x_i)$
则$val_i=\lim\limits_{x\rightarrow x_i}\frac{M(x)}{x-x_i}=\lim\limits_{x\rightarrow x_i}\frac{M’(x)}{(x-x_i)’}=\lim\limits_{x\rightarrow x_i}M’(x)=M’(x_i)$
于是我们可以用多点求值求出$val$数组。
现在讲拉格朗日插值的代数式恒等变形:
用分治$ntt$解决即可。
下降幂多项式乘法
考虑求出如下两个多项式的乘积:
$A(x)=\sum_{i=0}^na_ix^{\underline i},B(x)=\sum_{i=0}^mb_ix^{\underline i}$
然后考虑把它们转成点值形式然后乘起来再转回去。
设现在$F(x)=\sum_{i=0}^nf_ix^{\underline i},\hat F(x)$为其点值的生成函数。
现在先考虑$x^{\underline n}$的$EGF$
然后有
于是就转化成了常规多项式乘法问题。
我们把$\sum_{i=0}^{n}f_ix^i$这个多项式与$e^x$相乘就能得到点值的生成函数,同理,点值的生成函数乘上$e^{-x}$就能还原多项式。
因此可以结合$ntt/$暴力多项式乘法在$O(n\log n)/O(n^2)$的时间内完成下降幂多项式乘法。
普通多项式转下降幂多项式
已知普通多项式$A(x)=\sum_{i=0}^na_ix^i$
现在求下降幂多项式$B(x)=\sum_{i=0}^nb_ix^{\underline i}$使得$A(x)=B(x)$
思路:
考虑先多点求值,然后$iffp$即可求出对应的下降幂多项式。
下降幂多项式转普通多项式
已知下降幂多项式$A(x)=\sum_{i=0}^na_ix^{\underline i}$
现在求普通多项式$B(x)=\sum_{i=0}^nb_ix^i$使得$A(x)=B(x)$
思路:
考虑先$ffp$转点值,然后快速插值即可求出对应的普通多项式。
